

Comprendre l'Abaque de Smith par l'image
Introduction
Cette article est volontairement simple, le but n'étant pas de rentrer dans des formules de calcul complexes mais de montrer par l'image comment va évoluer l'impédance d'une antenne en fonction des modifications que l'on va lui apporter.J'ai utilisé pour les graphiques la version de démo de Smith V4 de l'auteur Fritz Dellsperger, un excellent logiciel pour apprendre le fonctionnement de l'abaque de Smith
Pour ce type analyses le NanoVNA est un formidable outils.
L'antenne radio
Les antennes ne sont pas de simple résistance R, mais des circuits avec une impédance complexe Z variant avec la fréquence.Celle-ci s'écrit ici :
Z = R + jX
jX est la réactance inductive ou réactance capacitive (qui doit être le plus proche de 0)
Abaque de Smith
L'abaque de Smith est un nomogramme, c'est à dire un outil graphique de calcul constitué de courbes graduées. Il va permettre d'avoir une représentation de l'impédance Z d'une antenne pour une fréquence ou plage de fréquence donnée, mais permet aussi de faire des calculs de correction (non traités ici).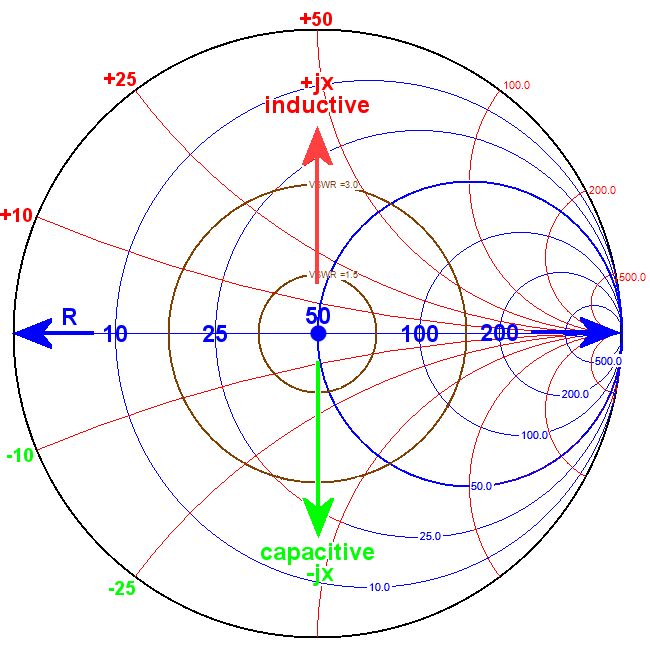
Point important :
- L'abaque est utilisé pour une impédance de référence, ici 50 Ohms
- Dans les exemples ci-dessous, la fréquence de référence est de 435MHz
Le point central 50 est l'antenne idéale avec R=50 Ohms, ni inductive, ni capacitive, le SWR=1 et s'écrit :
Z=50+j0
Les 2 cercles autour de ce point sont le SWR=1,5 et le SWR=3
En bleu on se déplace sur l'axe des résistance R :
cela donne par exemple :
Z=25+j0 ou Z=100+j0
En rouge l'antenne est trop inductive :
cela donne par exemple :
Z=50+j25
En vert l'antenne est trop capacitive :
cela donne par exemple :
Z=50-j25
Dans les exemples ci-dessous, nous avons appliqué une modification à l'antenne en on observe en P2 comment elle évolue.
Dans l'angle haut droit, le schéma équivalent.
Le trait noir est la ligne ou la courbe de correction possible.
Résistance en série (rarement utilisé)
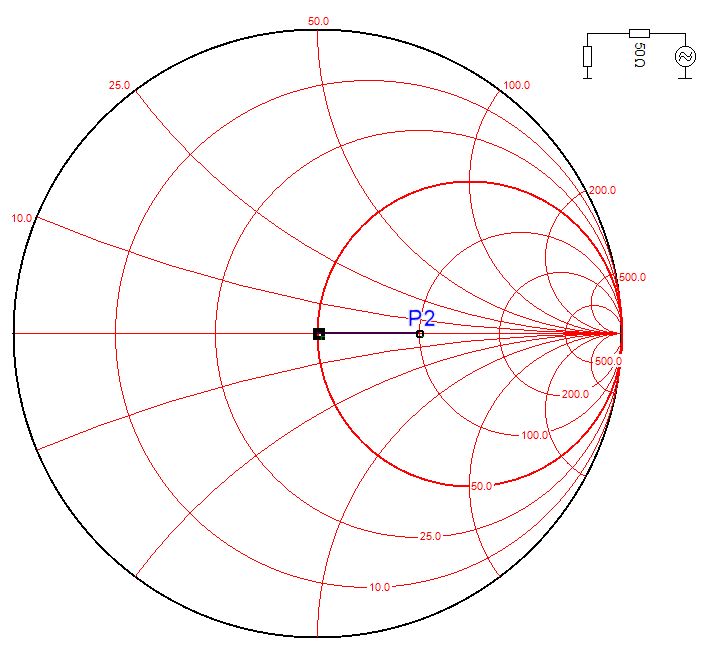
SWR=2
Z=100+j0
Résistance en parallèle (rarement utilisé)
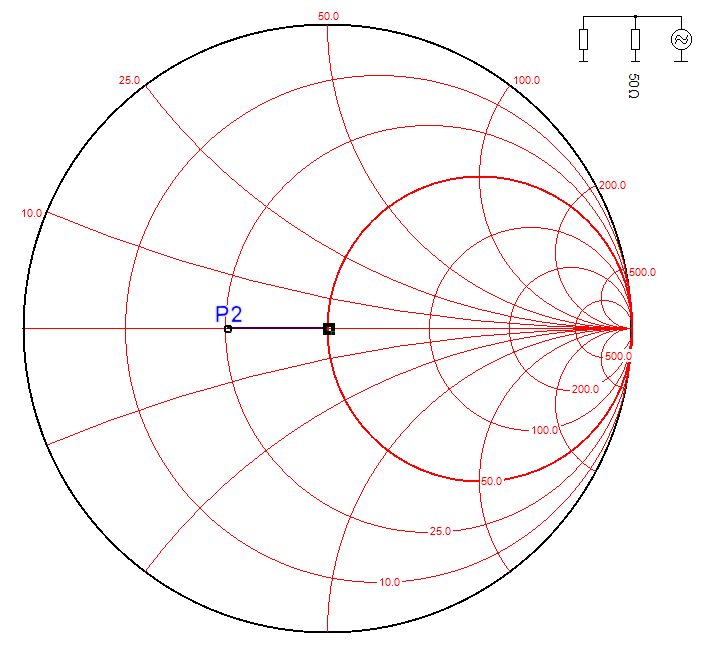
SWR=2
Z=25+j0
Inductance en série
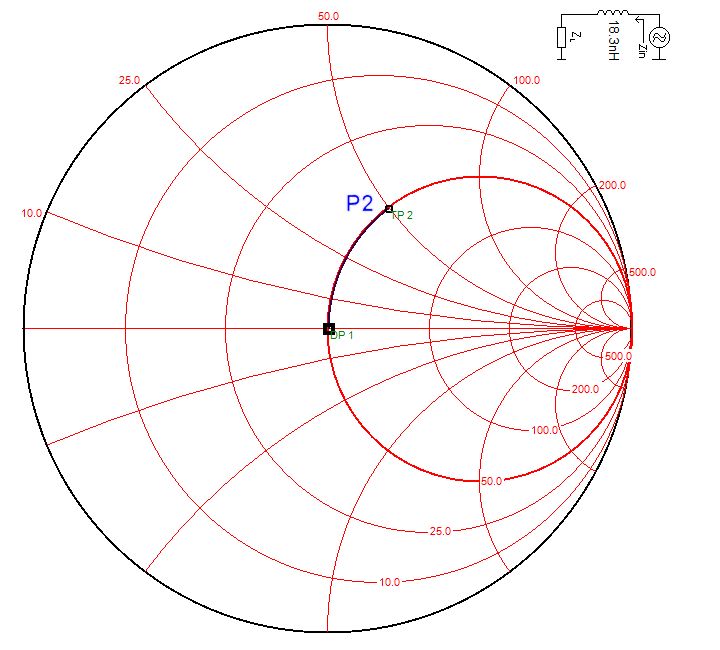
SWR=2.60
Z=50+j50
Inductance en parallèle
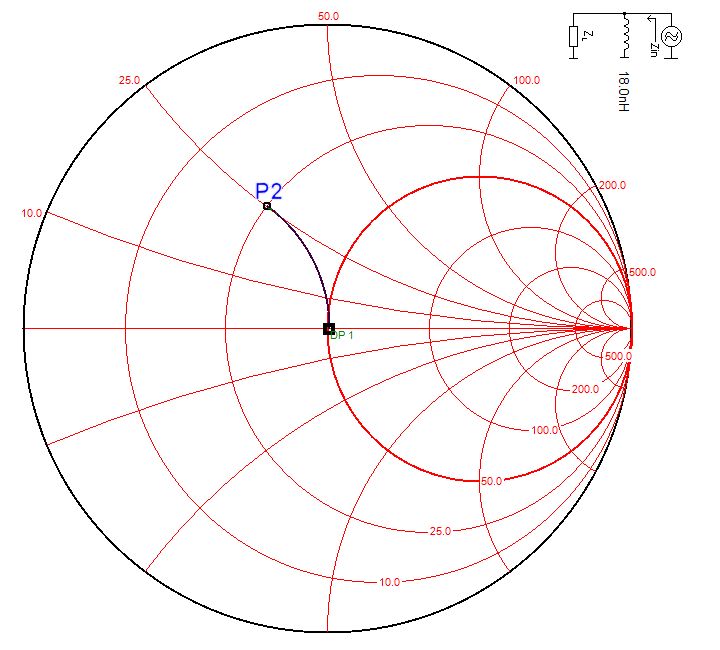
SWR=2.60
Z=50+j25
Capacité en série
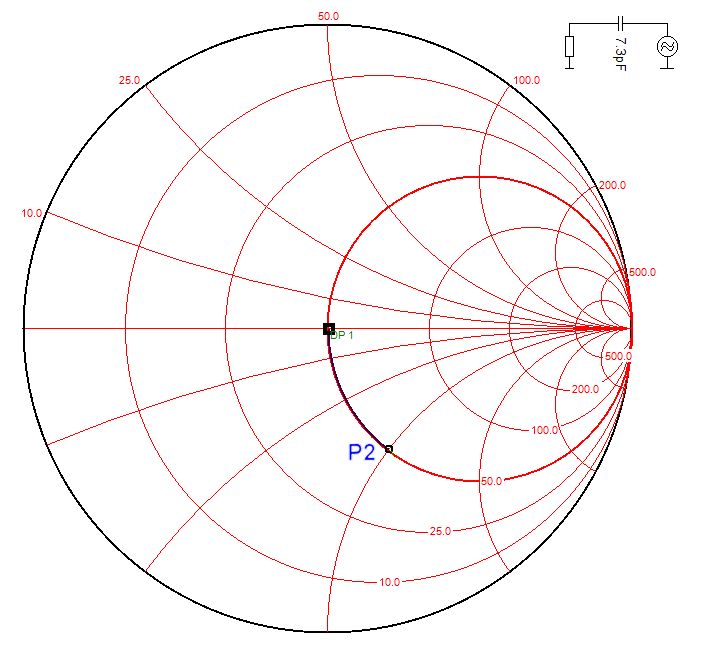
SWR=2.60
Z=50-j50
Capacité en parallèle
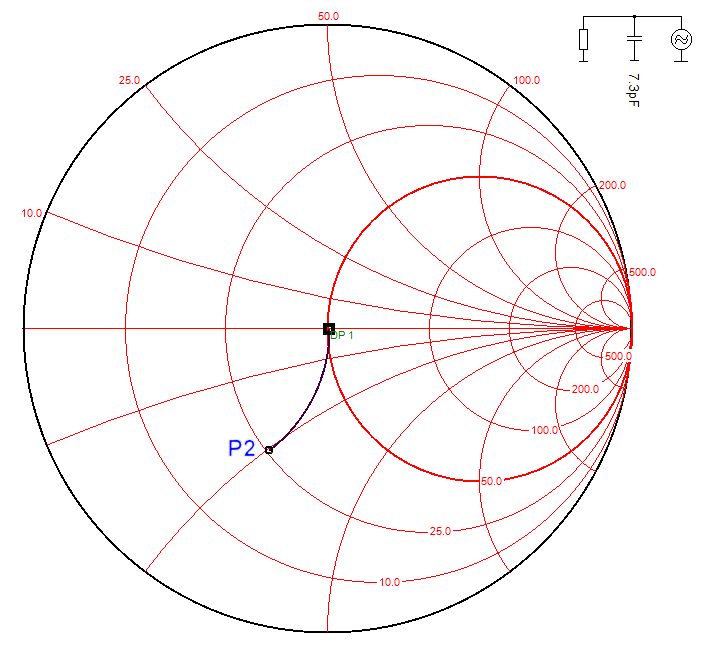
SWR=2.60
Z=50-j25
Transformateur (balun 1:4)
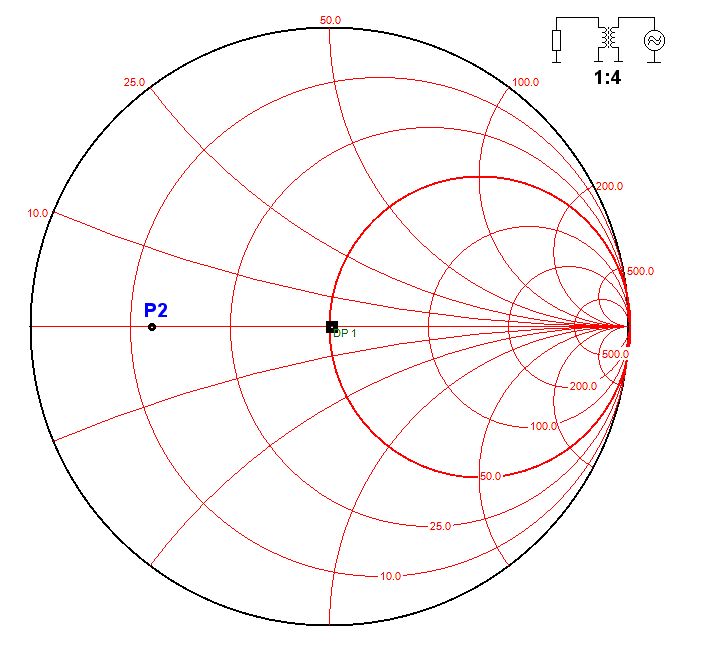
Le balun 1:4 (s'il est parfait) ne va modifier que la valeur de R :
50/4 = 12.5 Ohms
SWR=4.00
Z=12.5-j0
Information complémentaire
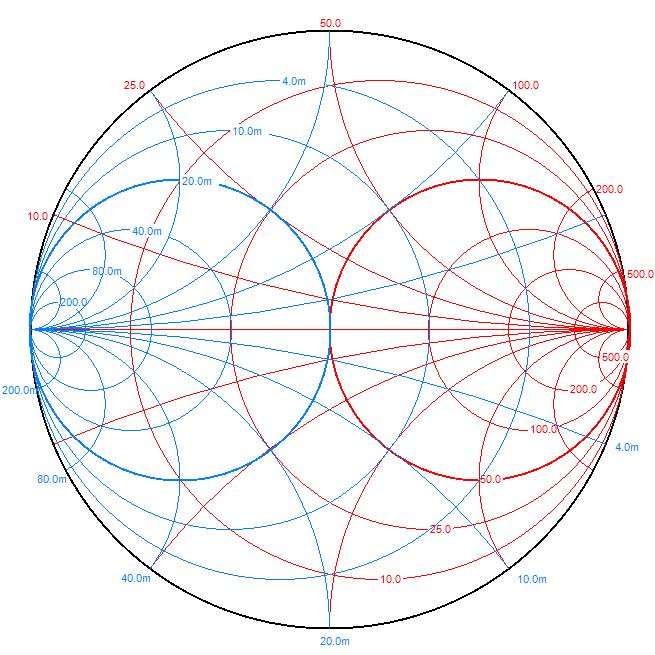
L'inductance et la capacité en parallèle ne semblent pas suivre les courbes ?
C'est normal car pour simplifier, je n'ai représenté que l'impédance Z.
L'abaque de Smith comprend en réalité aussi les courbes Y qui sont en quelque sorte le miroir de Z.
